Molecular Data
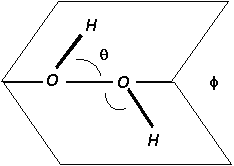
NOTE: The H2O2 molecule has no center of symmetry.
| Bond angles: |
Θ (H-O-O angle): 95° ± 2°
Φ (Dihedral angle): 120° ± 3°
Ref: Gmelin "Handbuch der Anorganischen Chemie", Suerstoff – syst. 3, Lief. 7-8 Auflage – Weinheim – VERLAG Chemie, p.429 (1966)
|
| Bond length: |
O-H: 0.097 ± 0.001 nm - Ref: P.A. Giguere and O. Bain, J.Phys.Chem. 56:340-42 (1952)
O-O: 0.149 ± 0.001 nm - Ref: S.C. Abrahams, et.al., Acta Cryst. 4:15-20 (1951)
|
| Bond strength: |
HO-OH: 51 ± 1 kcal/mole - Ref: J.A. Kerr, Chem.Rev. 66:465 (1966)
H-OOH: 90 ± 2 kcal/mole - Ref: J.A. Kerr, Chem.Rev. 66:465 (1966)
|
| Dipole moment: |
μ = 2.2 debyes
|
| |
Wave Number, cm-1 |
| Vibration |
O-H stretching |
3610 |
| Symmetric bending |
1295 |
| O-O stretching |
890 |
| Torsional oscillation |
520 |
| O-H stretching |
3610 |
| Unsymmetrical bending |
1266 |
| Moments of inertia (g.cm2) |
IA = 2.78 x 10-40 |
| IB = 34.0 x 10-40 |
| IC = 33.8 x 10-40 |
| Ired = IA/4 = 0.696 x 10-40 |
| Barrier restricting internal rotation: |
Vo = 3.5 kcal/mole |
| Absolute entropy: |
So298.16 = 55.66 cal/mole °K |
P.A. Giguere, I.D. Liu, J.S. Dugdale, J.A. Morrison. Can. J. Chem., 74:3715 (1952)
Notes:
- In rotation as a whole, the molecule remains rigid.
- Vibration may be considered to be harmonic oscillations.